【科学雑記】 無理を導き出す!√2の算出編
「よくはわからないがとにかくこういうものだ」と説明すると、なぜか妙に納得いってしまう事柄ってありませんか?
世界の有名な建物「ピサの斜塔」ですら、「ともかく傾いた塔だ」というと、理由とかを求めずになぜかそういうものかと納得してしまいます。

深く知ろうとする探求心の強い方は物事の「核心」を見つけようとすることが多いですが、反対に耳に入れておくだけというという方は「なんとなくの全体像を掴めれば良い」と思うことが多いと思います。
好きな漫画の作品を友達に勧めて、「なんでこういう展開になったの?」って聞かれたら「それはそういうもんやから…」とあきらめの意志もあるかもしれません
▼(とある漫画の例)

少しタイトルから反れてしまいましたが、今回は「こういう数だから仕方ない」といって話を割り切ってしまう無理数についてです。
無理数とは有理数でない実数で、分数の形で表せない数を指します。
ちなみに有理数は分数の形で表せる数です。
例えば、円周率のπや根号(√ )を含んだ数、ネイピア数のe、物理の世界では重力加速度g(観測された値に該当するため、無理数であることを証明する必要があるとの指摘があったため真偽は不明です。)など様々です。
こういった無理数は果たして「こういったものだから」で済ませない数だと思います。必ず何かしらの形で求めることによって得られた結果を見ているわけなので、今回はその無理数である√2をどうにかして算出したいと思います。

まずは、下図に直角三角形があります。
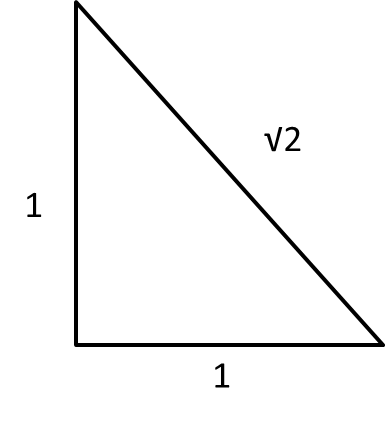
この直角三角形は三平方の定理より、1²+1²=√2²
移項すると、√2²-1²=1² となります
ここでa²-b²=(a+b)(a-b)より、
①:(√2+1)(√2-1)=1ですね。
②:①の式を変形すると、
| (√2-1) | = | 1 | |
| (√2+1) |
③:②から
| √2 | =1+ | 1 | |
|
(√2+1) |
④:√2に③の式を代入
| √2 | =1+ | 1 | |
|
(1+1/(1+√2)+1) |
つまり、
| √2 | =1+ | 1 | |
|
(2+1/(1+√2)) |
となります。
⑤:④の式の√2に③の式を代入
| √2 | =1+ | 1 | |
|
(2+1/(1+1+1/(1+√2))) |
つまり、
| √2 | =1+ | 1 | |
|
(2+1/(2+1/(1+√2))) |
となります。
⑥:⑤の式の√2に③の式を代入…を繰り返す。
と繰り返し計算していくときりがないので(無理数はこれがつらい)
ここで、1²<2<2²であるから、1<√2<2なので楽しましょう!
⑥の式でやめて、√2=1として近似します。
そしたら…
| √2 | =1+ | 1 | |
|
(2+1/(2+1/(1+1))) |
| √2 | =1+ | 1 | |
|
(2+1/(2+1/2)) |
| √2 | =1+ | 1 | |
|
(2+1/(5/2)) |
| √2 | =1+ | 1 | |
|
(2+2/5) |
| √2 | =1+ | 1 | |
|
(12/5) |
| √2 | =1+ | 5 |
|
12 |
√2=1.416となります。
これは本来の数字1.414とは少しかけ離れていますが、近い値となっています!
無理数を導き出せました!やってみるものです…

また、⑥でやめずに順々に繰り返していけばさらに正確な値が導けます。
しんどいもんで、こういった仕事はコンピューターに丸投げしたいものです。ですが、導けるということでも大きな一歩と言えましょう!

長くなりましたがいかがだったでしょうか?
これはこういうものだと思うものや事柄の核心を確かめることはとても大切です。
何事も結果があれば原因はあります。そこを追及する楽しさこそが科学なのかもしれませんね!
いつもご愛読ありがとうございます!
それでは!
参考文献:数研出版 赤チャート数学Ⅰ
